K近邻(K-Nearest Neighbor,KNN)分类算法是典型的监督性学习算法,是一种分类算法,也是最简单易懂的机器学习算法,没有之一。它采用测量不同特征值之间的距离方法进行分类。
它的思想很简单:计算一个点A与其他所有点之间的距离,取出与该点最近的K个点,然后统计这K个点中所属分类比例最大的,则点A属于该分类。简单来说就是由你的邻居来推断出你的类别。
首先,请看下图
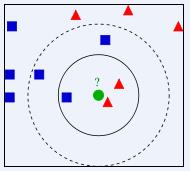
当K=3时,请问绿色圆形属于哪一类?
当K=5时,请问绿色圆形属于哪一类?
按照我们肉眼来看,粗糙判断当K=3时,绿色的圆属于红色三角形;当K=5时,绿色圆形属于蓝色正方形。
通过实例看K近邻分类算法

问:当K=3时,P(1.1,0.3)属于哪一类?
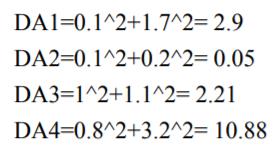
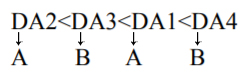
若K=3,则P属于A;
若K=2呢?
若K=4呢?
当K=2,4时,无法准确判断p到底属于A还是B,只能随机选取一个类别,这也是KNN的一个缺点,对此有个办法可以优化KNN分类算法,就是改进类别概率估计,根据A1、A2、A3和A4到P点距离进行加权计算,

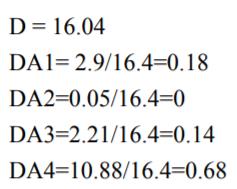
距离越小越相似,所以当K=2,3,4时,p分别属于A,A,A。
这只是从最基本的数字上来看K近邻分类算法,那在生活中如何运用K近邻分类算法呢?首先,小编归纳K-近邻算法的一般流程有以下:
(1)收集数据:可以使用任何方法。
(2)准备数据:距离计算所需要的数值,最好是结构化的数据格式
(3)分析数据:使用Matplotlib画二维扩散图
(4)训练算法:此步骤不适用于K-近邻算法
(5)测试算法:计算错误率
(6)使用算法:产生简单的命令行程序,输入一些特征数据测试。
注:在KNN中,通过计算对象间距离来作为各个对象之间的非相似性指标,避免了对象之间的匹配问题,此处距离使用了欧氏距离。
K-近邻算法属于惰性学习,但其计算复杂度较高,因为每进新样本,都需要与数据集中每个数据进行距离计算,计算复杂度和数据集中的数据数目n成正比;另一个是K的取值问题,K取不同值时,分类结果可能会有显着不同。一般K的取值不超过20,上限是n的开方。
那么问题来了,有的蝌蚪们可能不知道K的取值为何不超过20,小编找了一下可以让自己接受这个观点的理由,在此可以用Iris数据集稍微解释K的取值为何不超过20。(注意,此处幷非证明K不超过20)
Iris数据集是常用的分类实验数据集,由Fisher, 1936收集整理,也称鸢尾花卉数据集,是一类多重变量分析的数据集。数据集包含150个数据集,分为3类,每类50个数据,每个数据包含4个属性。可通过花萼长度,花萼宽度,花瓣长度,花瓣宽度4个属性预测鸢尾花卉属于(Setosa,Versicolour,Virginica)三个种类中的哪一类。
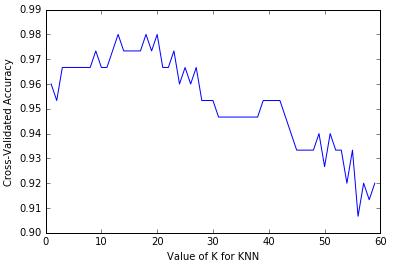
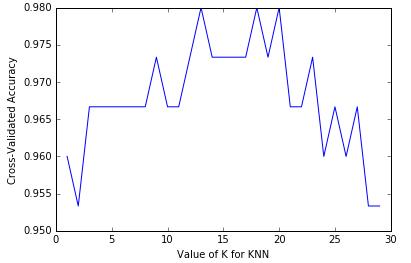
直接来看K的取值与预测准确性的关系图:
若K=60,有
若K=30,有
现在让小编带领蝌蚪们探索《机器学习实战》中一个很有意思的例子——海伦心中的那一位到底是谁?
下面我们来看具体操作:
海伦收集的数据是记录每位嘉宾的三个特征:每年获得的飞行常客里程数、玩视频游戏所消耗的时间百分比、每周消费的冰淇淋公升数。数据是txt格式文件,如下图,前三列依次是三个特征,第四列是分类(1:不喜欢的人,2:魅力一般的人,3:极具魅力的人),每一行代表一位嘉宾。
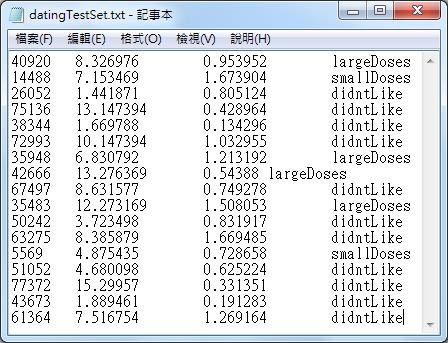
共有17条数据,需要将这些数据存到矩阵中,用矩阵来承装这些数据。
需要两个矩阵:一个承装三个特征数据,一个承装对应的分类。
于是,我们定义一个函数,函数的输入时数据文档(txt格式),输出为两个矩阵。

可以大概看下这17条数据的散点图分布:

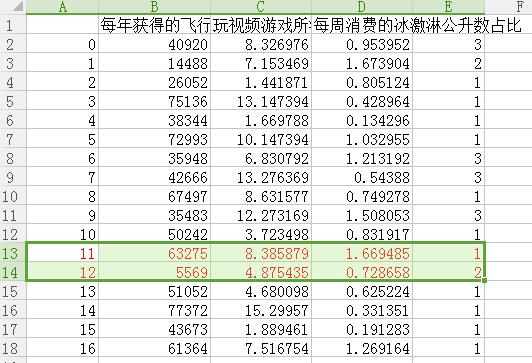
计算样本11和样本12之间的距离:
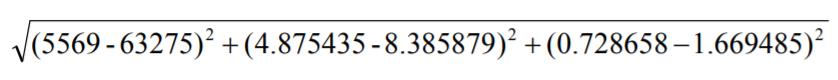
可以看到,每年获得的飞行常客里程数对于计算结果的影响远远大于其他两个特征。但这三个特征是同等重要的,因为我们采用方法是将数值归一化处理,取值范围为0,1之间或者-1到1之间。
公式:
newValue = (oldValue – min) / (max – min)

归一化后的数据:

接下来,我们测试算法:作为完整程序验证分类器。
首先将样本数据分一半为测试集,一半为训练集
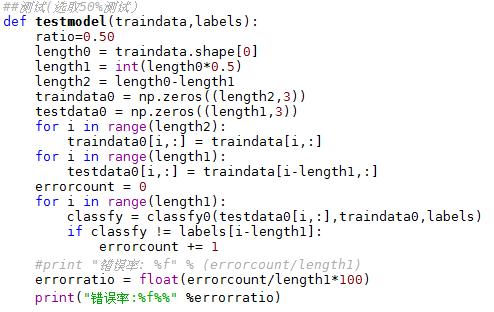
当K = 3时,当K = 4时,错误率是多少?
可以试一下,当K = 3时有:

而当K = 4 时,测试结果为12.500000%
可将K = 1,…9均进行测试,有:
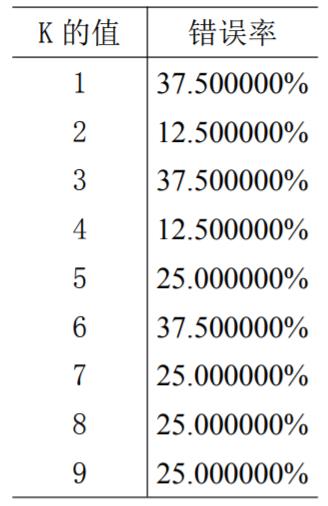
可以参考K = 2 或K = 4时错误率最低。

选K = 4,输入嘉宾每年获得的飞行常客里程数是:40000;每周消费的冰激淋公升数是:0.9;玩视频游戏所消耗时间:9。输出largeDoses 。有87.5%的把握可以认为这位嘉宾对海伦来说是极具魅力的人。
